文字列に効く動的計画法: レーベンシュタイン距離

この記事は「文字列に効く動的計画法」シリーズのレーベンシュタイン距離に関する記事です。

文字列の為の動的計画法

動的計画法(DP)は複雑な問題をより小さく単純な部分問題に分割し解決する手法です。その中には文字列メトリクスに対して効果的なパターンもいくつかあり、このシリーズはそれらに関する私のまとめノートです。何か追加すべきものがあると思われる場合は、お気軽にお問い合わせください。

• レーベンシュタイン距離: この記事です。
• 最長共通部分列(LCS)
• 正規表現
• Distinct Subsequence (coming soon)
• Longest Repeating Subsequence (coming soon)
• Hamming Distance (coming soon)

レーベンシュタイン距離

レーベンシュタイン距離はスペルチェックや文字列のあいまい検索に利用されており、以下のような状況の測定値を返します：

    文字列 A とターゲット文字列 B があります。文字列 A の文字を置き換え、挿入、削除することができる場合、文字列 A をターゲット文字列 B と同一にするために必要な修正数はいくつですか？

DP テーブル

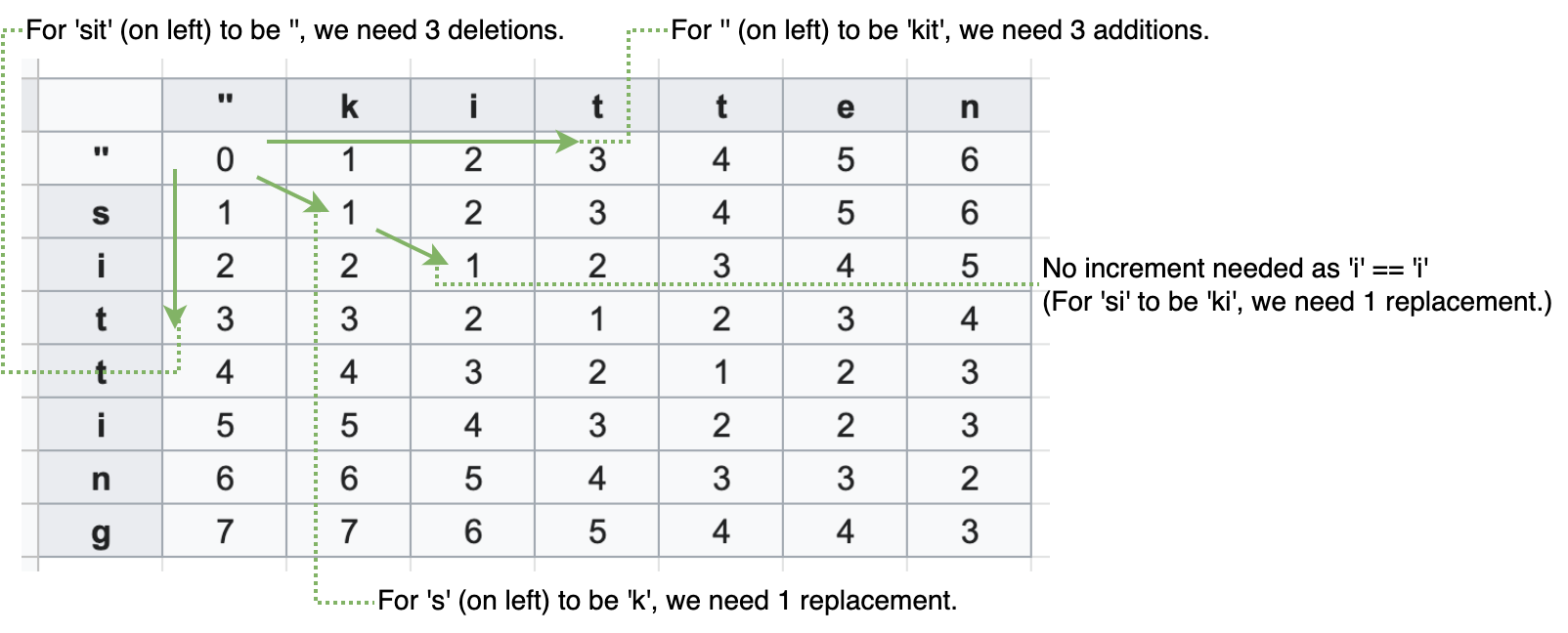
以下の表において、「sitting」（左側に垂直にマップされたもの）は比較対象の文字列であり、「kitten」（上部に水平にマップされたもの）はターゲット文字列です。空文字を基本ケースとするため、最初の行と列は 1 ずつ増加します。一行目でいうと、空文字を「kitten」にするには６文字の追加が必要な為です。

[1, 1]の位置から 2 つの文字を比較し、左から各セルを各行チェックしていきます。比較対象の文字列の観点から見ると水平増加は文字の追加を表し、垂直増加は削除を表します。そして左上から右下への斜め増加は文字の置き換えを意味しますが、文字が同一である場合、置き換えは必要無く、操作数は左上と同じままになります。

実装

def levenshtein(s, target):
    slen = len(s) + 1  # +1 for empty string
    tlen = len(target) + 1
    dp = [[0 for _ in range(tlen)] for _ in range(slen)]  # DP table creation

    for i in range(1, slen):  # base case of an empty character
        dp[i][0] = i
    for i in range(1, tlen):
        dp[0][i] = i

    for i in range(1, slen):
        for j in range(1, tlen):
            if s[i-1] == target[j-1]:  # if characters are identical, cost is 0
                substitute_cost = 0
            else:
                substitute_cost = 1
            dp[i][j] = min(dp[i-1][j] + 1,  # delete
                           dp[i][j-1] + 1,  # insert
                           dp[i-1][j-1] + substitute_cost)  # substitute

    return dp[-1][-1]