文字列に効く動的計画法: 正規表現チェック

この記事は「文字列に効く動的計画法」シリーズの正規表現チェックに関する記事です。

文字列の為の動的計画法

動的計画法(DP)は複雑な問題をより小さく単純な部分問題に分割し解決する手法です。その中には文字列メトリクスに対して効果的なパターンもいくつかあり、このシリーズはそれらに関する私のまとめノートです。何か追加すべきものがあると思われる場合は、お気軽にお問い合わせください。

• レーベンシュタイン距離
• 最長共通部分列(LCS)
• 正規表現チェック: この記事です。
• Distinct Subsequence (coming soon)
• Longest Repeating Subsequence (coming soon)
• Hamming Distance (coming soon)

DP を使った正規表現チェック

この問題は動的プログラミングを使って正規表現のマッチをチェックする問題です。正規表現といっても正確には文字の一致に加え「.」と「*」のパターンだけを含む簡素化されたものであり、実際の正規表現はより多くの構文をサポートしており、実装はより複雑です。

以下、パターン文字の説明です：

• 文字 = リテラルマッチ
• . = 任意の文字
• * = 一文字前の表現の 0 回以上の繰り返し（+は 1 回以上、?は 0 または 1 回）

リテラル文字のマッチングは、文字が正確な位置と順序にある必要があります。例えば、メタ記号のないパターンabcに一致する文字列はabcだけです。.の記号は任意の文字に一致します。この問題の中で少し特殊なのは*の記号です。*は一つ前の文字の繰り返しにマッチしますが、「一つ前の文字が一切ない（0 回起きる）」という状態もマッチします。例えば、abcccdという文字列がある場合、abc*dが一致するのは分かりやすい例ですが、abc*de*も一致します（e*はeが 0 回存在することもマッチするためです。）

DP テーブル

以下の表では、上部に水平にマップされたa.c*de*が正規表現パターン、左側に縦にマップされたabcccdがパターンに比較される文字列となります。空の文字を基本ケースとして定義しますので、文字マッチでは[0, 0]だけがtrueで、最初の行と列の残りのセルはすべてfalseになります。

各セルを[1, 1]の位置から右方向へ各行見ていきます。セル毎にパターン文字と対象文字を比較し、2 つの文字が一致する場合、セルを左上からの値で更新します。パターン文字が.である場合も同様 になります（任意の文字に一致するため）。この対角線方向に動く真偽値の繋がりがパターンマッチが有効かどうかを表し、この DP の結果となります。*のパターン文字には、異なる角度の検証が必要になります。まず現在見ているセルから 2 つ左の DP 値が必要です。これは前述した様に*が「一つ前の文字が一切無い（0 回起きる）」という状態を反映するためです。実はこの更新は一つ前の文字が実際の文字列に存在する場合にも重要な効果を発揮します。一つ前の文字の繰り返しが実際に起こった場合、一つ上の値で現在のセルを更新します。これは、繰り返しのパターン（例えばc*）の直前までマッチしている場合にのみ現在のセルがtrueになり、それがパターン全体のマッチ結果に繋がるわけです。そして最終的に一番右下のセルが結果となります。

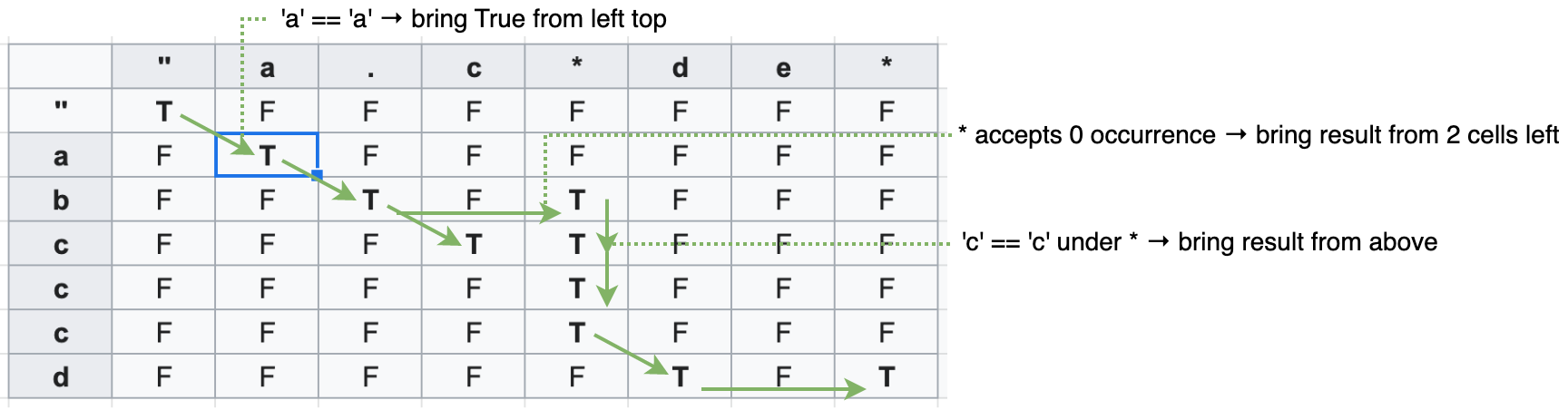
上記の DP テーブルがこの問題のメインロジックですが、実は別で検証すべきコーナーケースがあります。パターンがa*やa*b*c*のような繰り返しのマッチ表現のみを持つ場合、上記の DP テーブルで縦に更新したtrueの値が存在しなくなってしまいます。これは繰り返しのパターンの前に文字が無い為に起こります。このコーナーケースは DP テーブル全行を更新し始める前に、最初の行飲みを対象に 0 回出現のチェックをすることで解決できます。

実装

def regex(s, pattern):
    slen = len(s) + 1
    plen = len(pattern) + 1
    dp = [[False for _ in range(plen)] for _ in range(slen)]
    dp[0][0] = True

    for i in range(1, plen):  # handles sequential pattern in the first row
        if pattern[i-1] == '*':
            dp[0][i] = dp[0][i-2]

    for i in range(1, slen):
        for j in range(1, plen):
            if pattern[j-1] == '.' or pattern[j-1] == s[i-1]:  # '.' or char match
                dp[i][j] = dp[i-1][j-1]  # diagnal update
            elif pattern[j-1] == '*':  # sequence pattern
                dp[i][j] = dp[i][j-2]  # update for 0 occurence
                if pattern[j-2] == '.' or pattern[j-2] == s[i-1]:  # match before sequence pattern
                    dp[i][j] = dp[i-1][j]  # vertical update

    return dp[-1][-1]