This articles is about regular expression in a series of articles: DP for String Metrics.

Series: DP for String Metrics

Dynamic programming (DP) solves a complicate problem in optimal substructure by breaking it down into simpler sub-problems, and there are DP patterns that are very effective for string metrics. These articles are my summary notes on them. Please feel free to ping me for anything you think I should add.

Regular Expression with DP

This is a problem to check regular expression matching with dynamic programming. It’s actually a simplified regex with limited patterns including . , * and characters only. Real implementations of regular expression support more syntaxes and they are more complicated.

Following is the explanation of symbols:

  • character = literal match
  • . = any character
  • * = 0 or more of preceding expression (+ is 1 or more and ? is 0 or 1)

Literal character matching needs characters to be in an exact position and order. For example, a pattern of abc without any metacharacter matches only with abc. The metacharacter of . matches with any character, which seems straightforward. The metacharacter of * is a little tricky here. It matches with repeated occurrence of previous expression, but it also accepts 0 occurence. For example, having abcccd, a pattern of abc*d is a match, but abc*de* is also a match since e* means e can exist 0 time as well.

DP Table

In the table below, “abcccd” (vertically mapped on left) is the string to be checked with the pattern, “a.c*de*” (mapped horizontally on top). We define base cases to be empty character, so only [0, 0] is true for the character match and the rest of cells in the first row & column are all false.

We go through each cell from position [1, 1] to right every row, comparing each character against a pattern character. When the two characters match, the cell is updated with the value from above and left. The same goes when a pattern character is . since it matches with any character. This chain of bool values from top left to bottom right is the basis of this DP to judge if a pattern match happens or not. A pattern character of * requires checks of different angles. Firstly we need to bring a DP value of 2 cells left from a current cell. This is because * character accepts 0 occurrence of previous character. This update actually serves for actual occurrence of the previous character as well. When an actual sequence of a previous character happens, we update the current cell from one above, which would make the current cell true only when there’s a match before a sequential pattern such as c* starts. Finally we get the result at the last cell.

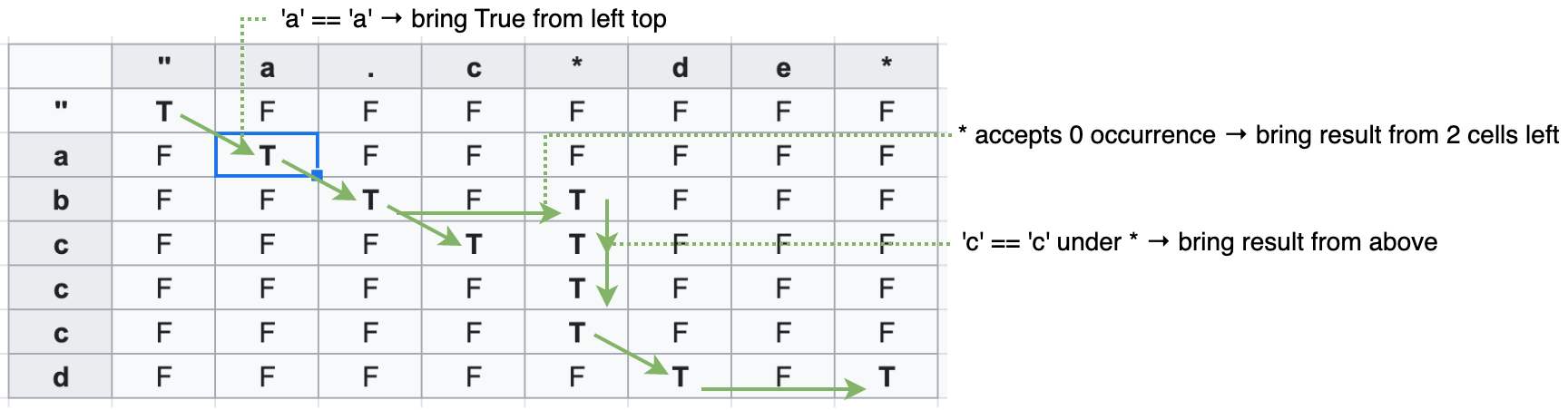
dp-regex-table

Before closing DP table explanation, there’s an edge case we need to handle actually. When a pattern has only sequential matches like a* or a*b*c* for example, we would not get the true value we vertically copied in the above case. So what we need is that 0 occurrence check we did in the example on the first row before starting DP table updates. This can be found in implementation below.

Implementation

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

def regex(s, pattern):
    slen = len(s) + 1
    plen = len(pattern) + 1
    dp = [[False for _ in range(plen)] for _ in range(slen)]
    dp[0][0] = True

    for i in range(1, plen):  # handles sequential pattern in the first row
        if pattern[i-1] == '*':
            dp[0][i] = dp[0][i-2]

    for i in range(1, slen):
        for j in range(1, plen):
            if pattern[j-1] == '.' or pattern[j-1] == s[i-1]:  # '.' or char match
                dp[i][j] = dp[i-1][j-1]  # diagnal update
            elif pattern[j-1] == '*':  # sequence pattern
                dp[i][j] = dp[i][j-2]  # update for 0 occurence
                if pattern[j-2] == '.' or pattern[j-2] == s[i-1]:  # match before sequence pattern
                    dp[i][j] = dp[i-1][j]  # vertical update

    return dp[-1][-1]