This articles is about Levenshtein Distance in a series of articles: DP for String Metrics.

Series: DP for String Metrics

Dynamic programming (DP) solves a complicate problem in optimal substructure by breaking it down into simpler sub-problems, and there are DP patterns that are very effective for string metrics. These articles are my summary notes on them. Please feel free to ping me for anything you think I should add.

Levenshtein Distance

This metric can be useful to things like spell checking or fuzzy string searches. It gives answers to the situation below:

    There are a subject string A and a target string B. How many fixes do we need to make string A identical to target string B when we can replace, insert or delete characters of string A?

(There is upper and lower bounds in terms of result value. Please check wikipedia page for the details.)

DP Table

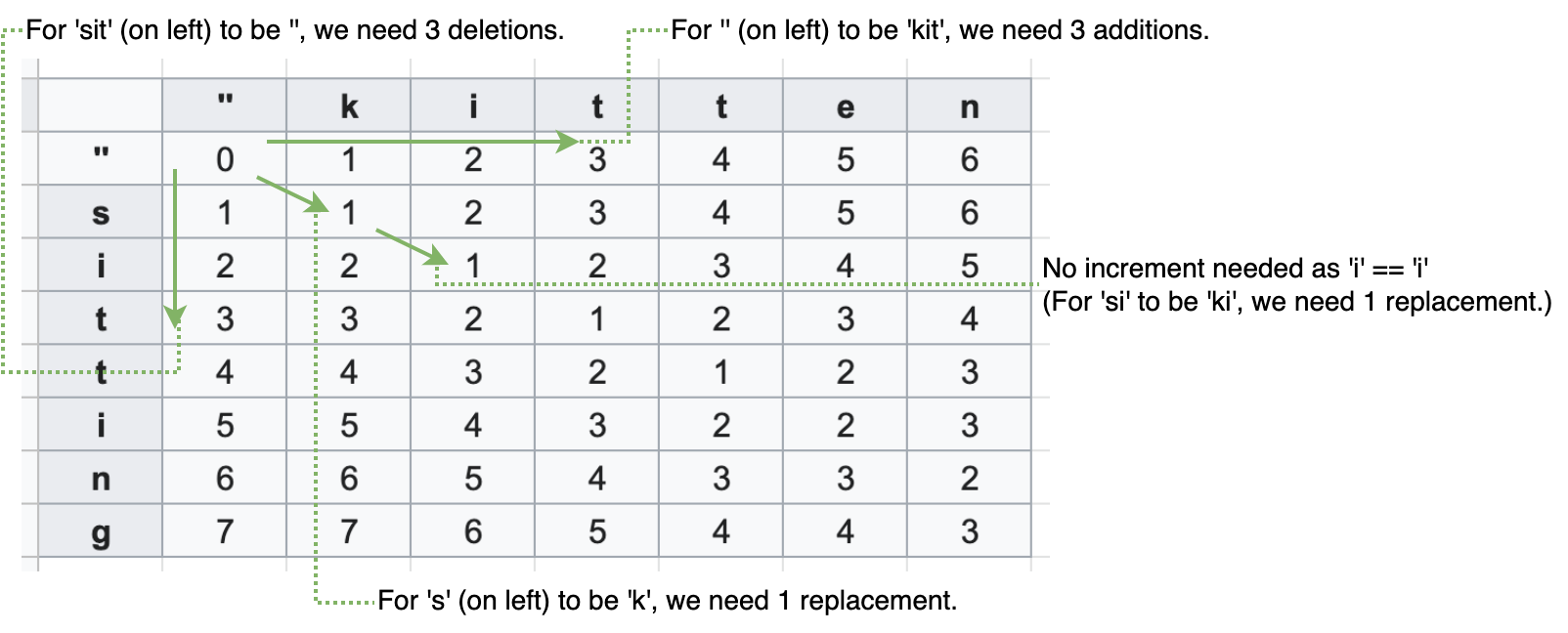
In the table below, “sitting” (vertically mapped on left) is the subject string to be compared against the target string, “kitten” (mapped horizontally on top). We define base cases to be empty character, so the first row and column increases one by one. (As to why, please refer to comments on the table.)

We go through each cell from position [1, 1] to right every row, comparing each character. From a perspective of the subject string, horizontal increments represent additions of characters and vertical increments represent deletions. Diagnal increments are somewhat special: they represents replacements of characters, and we do not require replacement when characters are identical to each other, in which case the operation count remains the same as the one above and left.

dax86-xv6

Implementation

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

def levenshtein(s, target):
    slen = len(s) + 1  # +1 for empty string
    tlen = len(target) + 1
    dp = [[0 for _ in range(tlen)] for _ in range(slen)]  # DP table creation

    for i in range(1, slen):  # base case of an empty character
        dp[i][0] = i
    for i in range(1, tlen):
        dp[0][i] = i

    for i in range(1, slen):
        for j in range(1, tlen):
            if s[i-1] == target[j-1]:  # if characters are identical, cost is 0
                substitute_cost = 0
            else:
                substitute_cost = 1
            dp[i][j] = min(dp[i-1][j] + 1,  # delete
                           dp[i][j-1] + 1,  # insert
                           dp[i-1][j-1] + substitute_cost)  # substitute

    return dp[-1][-1]