Dynamic programming (DP) solves a complicate problem in optimal substructure by breaking it down into simpler sub-problems, and there are DP patterns that are effective for string metrics. These articles are my summary notes on them. Please feel free to ping me for anything you think I should add.

List of Articles

Prerequisite

I tried to break things down as much as I could in the articles, however I’m not sure if they are granular enough to cover the fundamentals of DP itself. If you are not familiar with DP, knapsack problem would be a good starter for getting into DP. There are many materials online.

Keys for understanding: DP table initialization & update

There are multiple ways to solve problems with DP. Among them, this series uses a bottom-up approach exclusively. While top-down approach uses recursion, bottom-up approach uses a table (tabulation) which I find easier to visualize to understand the solutions.

Example of DP table (from Levenstein Distance)：

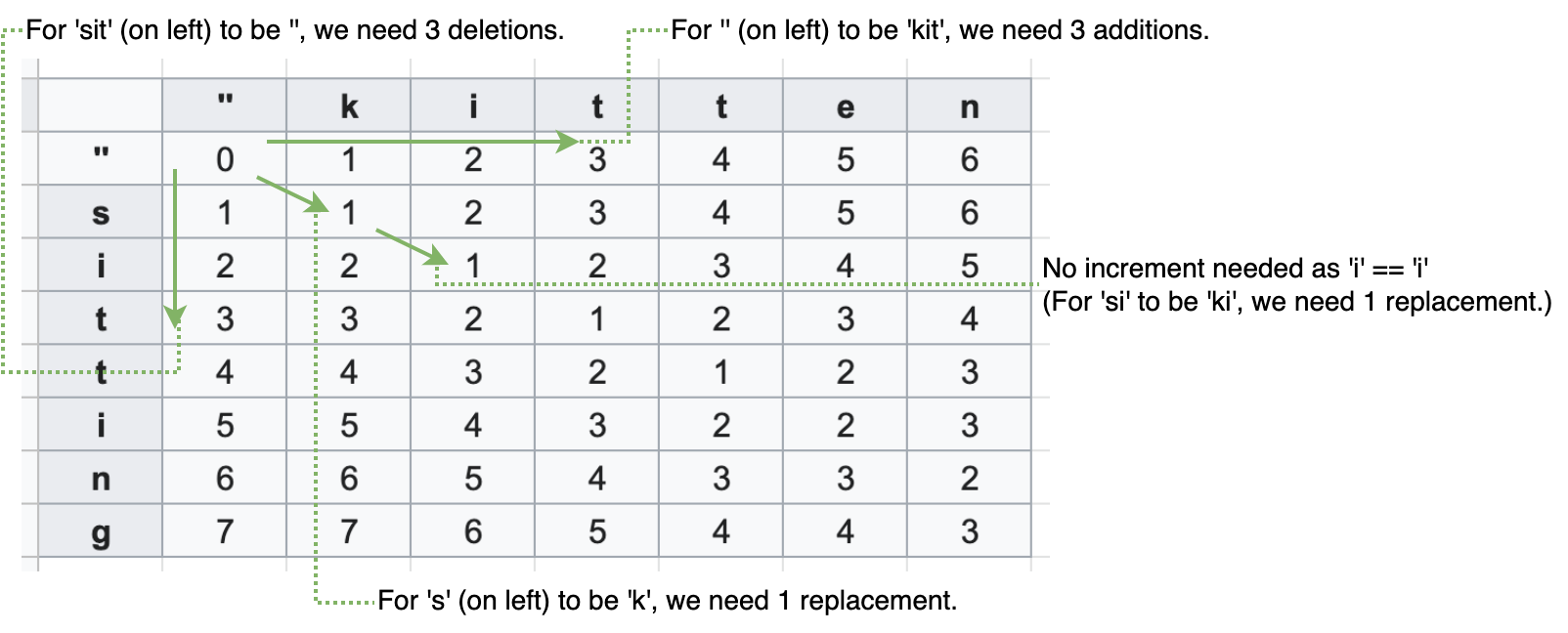
dax86-xv6

This series introduces DP patterns for different string metrics. At a glance they look somewhat similar, using table and all, however actual mechanism behind them is different to each one. The key difference to understand them is the meaning of values in a DP table, which makes table initialization and table update unique to each solution and worth paying our attention to.

Example codes of updating DP table:

1
2
3
4
5
6
7

if s[i-1] == target[j-1]:  # if characters are identical, cost is 0
    substitute_cost = 0
else:
    substitute_cost = 1
dp[i][j] = min(dp[i-1][j] + 1,  # delete
                dp[i][j-1] + 1,  # insert
                dp[i-1][j-1] + substitute_cost)  # substitute